Solutions
A spatio-temporal symmetry (the application of the relativity principle) is thus necessary, which enables the circularity of values’ exchanges, ensures a temporal continuity, which is non-discriminatory inside of the spatio-temporal reference frame, taking into account present and future while also limiting the quantity of money so it is both stable and a non-null exchange potential.
Is it even possible? Yes!
As we’ll see, not only the solution categories are perfectly determined but we can find one optimized solution.
a) Solution Classes
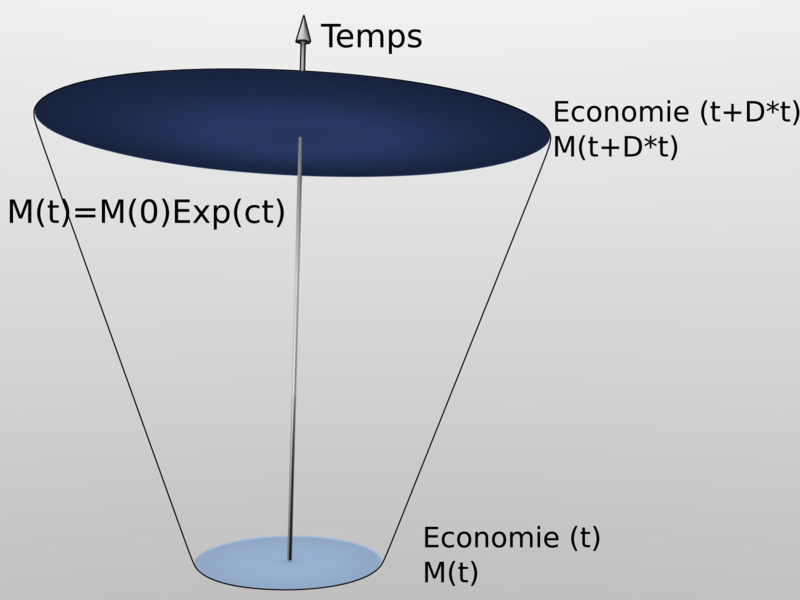
Monetary creation solutions respecting spatio-temporal symmetries imply that the money mass “M(t)” chosen by the actors is a mathematical mutual credit (not a debt), so without dimension and not linked to a specific value.
Symmetry conditions and thus of freedom, will permit us to establish the required differential equations to determine solutions to the “three producers” problem.
A spatial symmetry
No reference frame or individual present at an instant “t” is privileged regarding new money creation. We obtain then when “t” is constant:

dM represents money variation, and dx the spatial dimension and so with the definitions given in the previous chapters, the switch from one individual to another.
We are referring here to a notation and a reasoning as a physicist, but we could also have noted it in a more mathematical notation:

Everyone can then better understand the spatio-temporal symmetry invoked here according to their own usual notation and thinking referential.
A temporal symmetry
Every generation is established in the same economical way during all of its limited lifespan “ev”.
No generation is privileged over time. All individuals positioned at the time immediately following “t+dt” have to be credited with a relative part of money in the same way and in the same relative ratio than the individuals positioned at the time “t” and so in a continuous notation:

Or again with a discrete approach (dt = 1 time unit ):

“c” then represents the relative ratio or the relative variation of money during a small unit of time “dt” (we will see later what “small” means in our reasoning, when we will address the notion of lifespan).
The relative amount of money created must be then relatively constant at all times, thus respecting the temporal symmetry and allowing the participation of individuals of all generations to the same monetary system while respecting the three economic freedoms and the principle of relativity in the whole considered space-time.
This brings us to the fact that the “Three Producers Problem” is resolved by only one class of possible solutions. These are the exponential solutions (or “power” functions):

It is also written as a power of (1+c) in the form:

Concretely this means that for solutions that are coherent with the three economical freedoms and the principle of relativity, anyone of the N(t) actors of the economical zone existing at a date “t” is emitting a same relative part of money, a “universal dividend” (UD) that is valuated as:

In other words: the growth “c” of the money supply “M” is relatively stable and distributed symmetrically between all present and coming actors. These solutions with Universal Dividend ensure the respect of the relativity principle. The density of the money is guaranteed at all times as well as in space, avoiding that way the extreme monetary droughts (sources of deflation), as well as the extremes of the excess of monetization (sources of local bubbles or hyperinflation).
Money is created in a continuous way consistent with the continuous replacement of the generations and the growth of the chosen money supply, “c” is equitably attributed in space (the whole individuals) at a “t” instant whatever “t” is, which is the only way not to harm the economical actors both present and future ones, which we can also call “flow of individuals”.
So it is indeed the space-time factor, and more accurately the temporal dimension (generational), linked to the limited duration of the life of individuals, that changes the nature of the definition of the currency. So we need to avoid the fundamental error which is to consider all current actors as a “permanent” quantity. One must understand that it is a flow of individuals in perpetual renewal, and that in that flow there is no reason to favor any of them regarding the monetary creation in the whole economical space-time hereby determined.
“c” is the Universal Dividend factor, it represents a part of the total money supply existing at instant “t”, created for every member. That monetary part allows them to exchange their goods and services in a independent way from the previous monetary creation. That same part must be small enough in order for the pre-existing money to be maintained at a stable value.
It would be wrong to understand here that the money supply should be “an exponential function”. We have treated here only the theoretical case of the “Three Producers Problem”, perfectly replaced in space and time. Therefore we should only keep the fundamental instant result, namely a universal dividend for which we are going now to establish the limits and coherent framing values.
b) Optimization and Life Expectancy
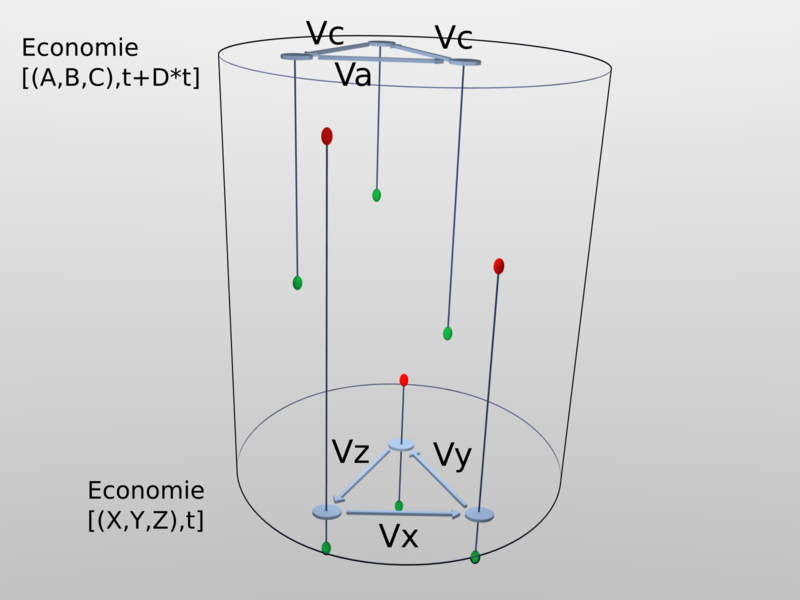
It is possible to find a fundamental relation between the Universal Dividend “c” and life expectancy. Indeed, to make it simple let’s consider first an economic zone composed of N(t) members with N(t) being stable in time and having an average life expectancy “ev”. Let’s observe at first how the living generation is positioning itself toward the flow between the generations that are already dead and those that are to be born.
If we imagine now that a unit of time passes, we must also see how individuals closer to “ev” go from life to death and those who are not yet born but soon to come to existence, as well as the transition from one time coordinate to the next of all those that stay alive.

In green, the living generations at “t”. We must see and understand on that diagram the temporal height of existence “ev” and its center of symmetry “ev/2”
To make an analogy, you can think of a fountain that always looks the same seen from a distance although its droplets of water disappear step by step with time, passing from the positions of those that are at initial projection at its base to those falling back in the pond. It takes a given time (the life span) for a drop of water to go through the whole “life track” by following the stream of the water jet, which itself seems immutable.
Once this observation is understood and put together with the previous results, we can then pose as a fundamental relation that the creation of the money supply during the whole past life expectancy should only be represented at the instant “t” compared to the existing money supply as the tiny fraction of individuals of that nearly disappeared generation but still present in the temporal height in the proportion of 1/ev.
We have to establish that:

Which implies:

Which gives us for c:

“c” being small we mathematically demonstrate (limited development) that it can also be written as:

Or more simply:

These last three expressions (E1), (E2) and (E3) being equivalent.
As we have noted before we cannot be totally satisfied with this value because the center of the temporal symmetry is placed at ev/2 and not at ev. It is thus here a minimal value for c, that goes in the way of giving the advantage to the leaving generation (the older ones). The same reasoning for “ev/2” gives us a value in accordance with central symmetry:

It is important to note that the time unit used in the calculation is not neutral, because it is linked to the regular distribution of the universal dividend in the economy. And this rhythm is not neutral for the economy. We choose the year as a fundamental economic unit because of experimental data that gives to the solar year a fundamental economic rhythm due to the annual harvest cycle as well as holidays.

The generation shown here in blue represents only 1/ev of the whole living people, has contributed to the monetary creation of the previous generation for M(t) during all its existence even if the money supply in place is M(t+ev)
Let’s note that money is quantitative when we use it, its continuous aspect being only an appearance (see the analogy of the fountain). Therefore, the computed Universal Dividend is quantitative. Having bounds of relative values is completely coherent with a stable quantitative UD which is recalculated and increased only when it is likely to exceed the acceptable bounds of its relative value. This remark is important and needs to be analyzed deeply. This is what allows a project of free money compatible with the RTM (like OpenUDC and uCoin - TN: currently Duniter) to use a fundamental, and yet simple and understandable, rule to arbitrate indefinitely between quantitative and relative value.
Conclusion
We can now conclude and completely write the fundamental result of the RTM:
**The monetary systems which are compatible with the principle of relativity and the three economic freedoms are monetary systems with a Universal Dividend whose value is a proportion “c” of the money supply which depends on the average human lifetime of the considered economic zone. The equation to calculate the UD should then be similar to:
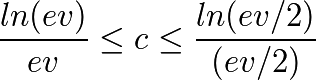
The contraposition is then also a fundamental result of the RTM:
“The monetary systems which do not integrate a universal dividend are not compatible with the relativity principle and the three economic freedoms”
To clarify it even better, we could also add that a universal dividend which would exist but would be too weak or too strong, outside of the defined ranges, on a too long period, thus favoring a generation over another (new, old, anyway!) would not be compatible with the RTM either.
This last point is fundamental because there is a great temptation for the living to claim excessive property rights on the living area, thus violating the freedoms of their successors. History is full of these violations of fundamental principles, which inevitably lead to rebellion on the long term.
We could remember that the Universal Dividend is almost inversely proportional to the life expectancy of the considered economic zone (ln being a function which varies very little).
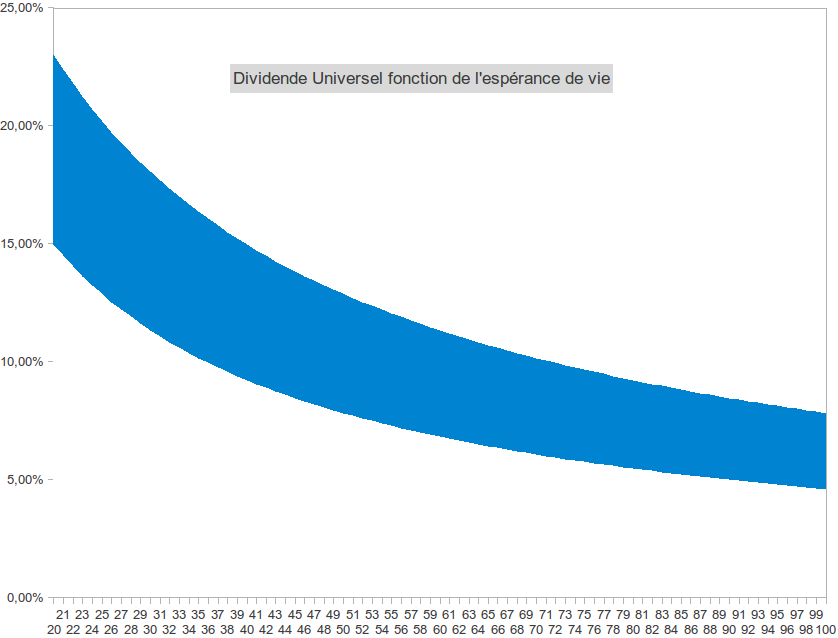
Acceptable values (in blue) of the % of universal dividend depending on the life expectancy. At the bottom of the colored area a too weak dividend will have a tendency to favor outgoings, whereas at the top a too high dividend will have a tendency to favor newcomers
These results conclude our main theoretical development.