Module Galilée¶
Le module Galilée est le premier module à réaliser en vue de la compréhension de la Théorie Relative de la Monnaie.
https://rml.creationmonetaire.info/modules/
Au lieu d’utiliser un tableur classique, je propose de profiter de l’occasion pour monter en compétence sur la bibliothèque Python nommée Pandas, qui permet de traiter de gros volume de données comme dans un tableur mais en code Python. Elle inclut les fonctions de la bibliothèque de création de graphiques Mathplotlib, permettant d’afficher simplement les graphiques correspondants aux données.
Le module a été entièrement réalisé dans un navigateur web avec JupyterLab.
Cette réalisation a été faîtes à quatre mains, j’ai réalisé la base avec quelques erreurs. Cuckooland a corrigé et amélioré tous les codes ! Je l’en remercie chaleureusement.
Je vous invite à consulter son site permettant d’approndir vos connaissances sur la Théorie Relative de la Monnaie.
(a) Changements de référentiels dans l’espace¶
Paramètres de la monnaie¶
Le premier tableur va nous permettre d’afficher les paramètres de la monnaie libre simulée. Nous avons donc :
ev : espérance de vie
c : taux de croissance annuel de la masse monétaire
N : nombre d’utilisateurs de la monnaie
DU0 : montant du premier DU
import pandas as pd
import math
pd.set_option('display.max_rows', 7)
# Paramètres de la monnaie
ev = 80
c = 0.1 # math.log(ev/2)/(ev/2)
N0 = 3
DU0 = 1000
account0 = DU0 / c
def get_du(c: float, M: [float], N: [int], DU: [float], i: int) -> float:
if (i == 1):
return DU0
else:
# formule de base du DU
#return c * (M[i-1] / N[i])
# formule DUĞ du DU
return DU[i-1] + (math.pow(c, 2) * (M[i-2] / N[i-2]))
def is_alive(age: int) -> bool:
return age >= 0 and age < 80
# Tableur des paramètres
params = pd.DataFrame({'EV': ev, 'c': c, 'N': N0, 'DU(t0)': DU0}, index=['Paramètres'])
# Affichage tableur
display(params)
| EV | c | N | DU(t0) | |
|---|---|---|---|---|
| Paramètres | 80 | 0.1 | 3 | 1000 |
Tableur d’une monnaie libre en quantitatif avec I1, I2, I3 sur 80 ans¶
# Initialisation des colonnes
years = list(range(1,ev+1))
account1 = [0]
account2 = [account0]
account3 = [2 * account0]
M = [account1[0] + account2[0] + account3[0]]
N = [N0]
average = [int(M[0] / N[0])]
DU = [float('nan')]
full_average = [float('nan')]
# Remplissage des colonnes
for i in range(1, ev):
N.append(N0)
new_DU = get_du(c, M, N, DU, i)
account1.append(account1[i-1] + new_DU)
account2.append(account2[i-1] + new_DU)
account3.append(account3[i-1] + new_DU)
M.append(account1[i] + account2[i] + account3[i])
DU.append(new_DU)
full_average.append(new_DU / c * (1 + c))
average.append(M[i] / N[i])
# Remplissage du tableur
accounts = pd.DataFrame(years, columns=['Année'], index=years)
accounts['I1'] = account1
accounts['I2'] = account2
accounts['I3'] = account3
accounts['Masse Monétaire'] = M
accounts['N'] = N
accounts['Moyenne'] = average
accounts['Moyenne Pleine'] = full_average
accounts['DU'] = DU
# Affichage tableur
display(accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.000000e+00 | 1.000000e+04 | 2.000000e+04 | 3.000000e+04 | 3 | 1.000000e+04 | NaN | NaN |
| 2 | 2 | 1.000000e+03 | 1.100000e+04 | 2.100000e+04 | 3.300000e+04 | 3 | 1.100000e+04 | 1.100000e+04 | 1.000000e+03 |
| 3 | 3 | 2.100000e+03 | 1.210000e+04 | 2.210000e+04 | 3.630000e+04 | 3 | 1.210000e+04 | 1.210000e+04 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 1.537993e+07 | 1.538993e+07 | 1.539993e+07 | 4.616980e+07 | 3 | 1.538993e+07 | 1.538993e+07 | 1.399085e+06 |
| 79 | 79 | 1.691893e+07 | 1.692893e+07 | 1.693893e+07 | 5.078678e+07 | 3 | 1.692893e+07 | 1.692893e+07 | 1.538993e+06 |
| 80 | 80 | 1.861182e+07 | 1.862182e+07 | 1.863182e+07 | 5.586546e+07 | 3 | 1.862182e+07 | 1.862182e+07 | 1.692893e+06 |
80 rows × 9 columns
Graphique en quantitatif¶
import matplotlib.pyplot as plt
# Courbes sur le même graphique
ax = plt.gca()
accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
accounts.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
accounts.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
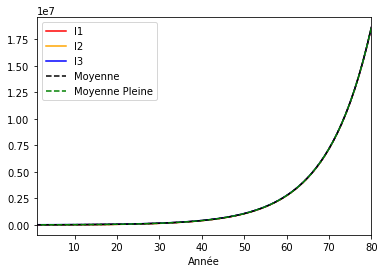
En quantitatif, c’est à dire en unités brutes, chaque utilisateur crée autant de monnaie. Nous avons là une démonstration de la “symétrie spatiale” (égalité de création monétaire entre les utilisateurs à un instant t). Avec des comptes ayant des montants différents, ils suivent tous la moyenne dans ce graphique, à première vue.
La masse monétaire, comme les comptes, augmente de manière exponentielle.
Faisons un zoom par une mise à l’échelle logarithmique de l’axe Y, pour voir pourquoi les comptes sont cachés sous la moyenne :
# Courbes sur le même graphique
ax = plt.gca()
accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
accounts.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
accounts.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
# Echelle logarithmique de l'axe Y
plt.yscale("log")
plt.show()
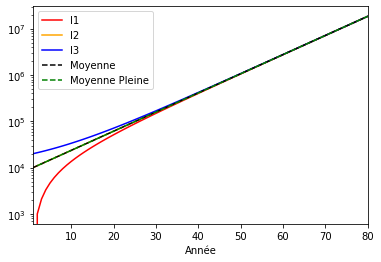
A cette échelle logarithmique, on s’aperçoit que les comptes convergent vers la moyenne !
Le compte I3 qui démarre à zéro, atteint la moyenne aux alentours de 40 ans, soit une demi espérance de vie. Statistiquement, 40 ans est la durée de vie moyenne pour une population avec une espérance de vie de 80 ans.
Etablir le référentiel relatif¶
# Capture de la colonne DU
du_series = accounts['DU']
# Nouveau tableur relatif
rel_accounts = accounts.copy()
for label, series in rel_accounts.items():
if label == 'Année' or label == "N":
continue
rel_accounts[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(rel_accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | 3 | NaN | NaN | NaN |
| 2 | 2 | 1.000000 | 11.0 | 21.000000 | 33.0 | 3 | 11.0 | 11.0 | 1.0 |
| 3 | 3 | 1.909091 | 11.0 | 20.090909 | 33.0 | 3 | 11.0 | 11.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 10.992852 | 11.0 | 11.007148 | 33.0 | 3 | 11.0 | 11.0 | 1.0 |
| 79 | 79 | 10.993502 | 11.0 | 11.006498 | 33.0 | 3 | 11.0 | 11.0 | 1.0 |
| 80 | 80 | 10.994093 | 11.0 | 11.005907 | 33.0 | 3 | 11.0 | 11.0 | 1.0 |
80 rows × 9 columns
Graphique en relatif¶
# Courbes sur le même graphique
ax = plt.gca()
rel_accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
rel_accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
rel_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
rel_accounts.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
rel_accounts.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
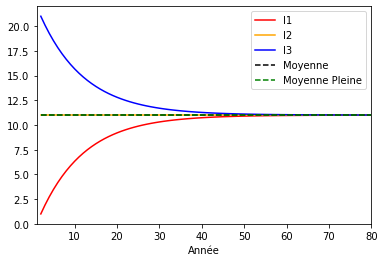
En relatif, on voit bien la convergence des comptes vers la moyenne. La moyenne qui se stabilise à 11 DU. En relatif, la moyenne reste stable au cours du temps, pour N constant toutefois. Il n’y a pas d’inflation de la masse monétaire, pas de création de monnaie, pas de destruction de monnaie !
Le compte I3 qui démarre à zéro, atteint la moyenne aux alentours de 40 ans, soit une demi espérance de vie. Ce compte a créé de la monnaie pendant 40 ans en relatif. Si les générations qui suivent créent le même nombre de dividende pendant la même durée, alors nous aurons une “symétrie temporelle”, c’est à dire une égalité devant la création monétaire entre générations.
Etablir le référentiel quantitatif à somme nulle¶
# Capture de la colonne Moyenne
average_series = accounts['Moyenne']
# Nouveau tableur quantitatif à somme nulle
sum_zero_accounts = accounts.copy()
sum_zero_accounts['Masse Monétaire'] = 0
for label, series in sum_zero_accounts.items():
if label.startswith('I'):
sum_zero_accounts[label] = series.sub(average_series).astype('float64')
sum_zero_accounts['Masse Monétaire'] = sum_zero_accounts['Masse Monétaire'] + sum_zero_accounts[label]
sum_zero_accounts['Moyenne Pleine'] = sum_zero_accounts['Moyenne Pleine'].sub(average_series).astype('float64')
sum_zero_accounts['Moyenne'] = sum_zero_accounts['Masse Monétaire'] / 3
# Affichage tableur
display(sum_zero_accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | -10000.0 | 0.000000e+00 | 10000.0 | 0.000000e+00 | 3 | 0.000000e+00 | NaN | NaN |
| 2 | 2 | -10000.0 | 0.000000e+00 | 10000.0 | 0.000000e+00 | 3 | 0.000000e+00 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | -10000.0 | 0.000000e+00 | 10000.0 | 0.000000e+00 | 3 | 0.000000e+00 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | -10000.0 | -1.862645e-09 | 10000.0 | -5.587935e-09 | 3 | -1.862645e-09 | 1.862645e-09 | 1.399085e+06 |
| 79 | 79 | -10000.0 | 0.000000e+00 | 10000.0 | 0.000000e+00 | 3 | 0.000000e+00 | 3.725290e-09 | 1.538993e+06 |
| 80 | 80 | -10000.0 | 0.000000e+00 | 10000.0 | 0.000000e+00 | 3 | 0.000000e+00 | 3.725290e-09 | 1.692893e+06 |
80 rows × 9 columns
Graphique en quantitatif à somme nulle¶
# Courbes sur le même graphique
ax = plt.gca()
sum_zero_accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
sum_zero_accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
sum_zero_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
sum_zero_accounts.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_accounts.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()

En quantitatif à somme nulle, c’est à dire en retirant la moyenne (M/N) à chaque compte, ceux-ci ont un montant fixe !
Non seulement la convergence des comptes vers la moyenne disparaît, mais le Dividende Universel aussi ! On peut représenter l’évolution du DU accompagnée de celle du compte d’I3 :
# Courbes sur le même graphique
ax = plt.gca()
sum_zero_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
sum_zero_accounts.plot(kind='line', x='Année', y='DU', color='magenta', ax=ax)
# Echelle logarithmique de l'axe Y
plt.yscale("log")
plt.show()

Pour comparer avec le DU, le mieux est de passer dans le référentiel relatif au DU.
Etablir le référentiel relatif à somme nulle¶
# Capture de la colonne DU
du_series = accounts['DU']
# Nouveau tableur relatif à somme nulle
sum_zero_rel_accounts = sum_zero_accounts.copy()
for label, series in sum_zero_rel_accounts.items():
if label == 'Année' or label == 'N':
continue
sum_zero_rel_accounts[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(sum_zero_rel_accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | 3 | NaN | NaN | NaN |
| 2 | 2 | -10.000000 | 0.000000e+00 | 10.000000 | 0.000000e+00 | 3 | 0.000000e+00 | 0.000000e+00 | 1.0 |
| 3 | 3 | -9.090909 | 0.000000e+00 | 9.090909 | 0.000000e+00 | 3 | 0.000000e+00 | 1.653627e-15 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | -0.007148 | -1.331331e-15 | 0.007148 | -3.993993e-15 | 3 | -1.331331e-15 | 1.331331e-15 | 1.0 |
| 79 | 79 | -0.006498 | 0.000000e+00 | 0.006498 | 0.000000e+00 | 3 | 0.000000e+00 | 2.420602e-15 | 1.0 |
| 80 | 80 | -0.005907 | 0.000000e+00 | 0.005907 | 0.000000e+00 | 3 | 0.000000e+00 | 2.200547e-15 | 1.0 |
80 rows × 9 columns
Graphique en relatif à somme nulle¶
# Courbes sur le même graphique
ax = plt.gca()
sum_zero_rel_accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
sum_zero_rel_accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
sum_zero_rel_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
sum_zero_rel_accounts.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_rel_accounts.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
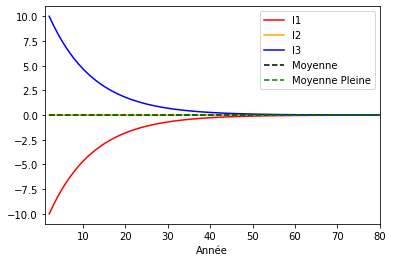
En relatif à somme nulle, la convergence des comptes vers la moyenne (sous l’effet du DU) réapparaît !
Comparaison du relatif avec un système de taxes redistribuées¶
Formule de la taxe¶
taxe individuelle(t) = c*(R(t)+1)/(1+c)
Formule de la redistribution¶
R(t+1) = R(t) + (taxe collectée(t) / 3) - taxe individuelle(t)
def get_taxe(c: float, R: int) -> float:
return c*(R+1)/(1+c)
def get_redistribution(c: float, N: int, R: float, taxe: float, collected: float) -> float:
return R + (collected / N) - taxe
# Nouveau tableur relatif par taxes
taxes_rel_accounts = rel_accounts.copy()
taxes_rel_accounts.drop('DU', axis=1, inplace=True)
taxes_rel_accounts.drop('Moyenne Pleine', axis=1, inplace=True)
# Initialisation des colonnes
account1 = [0]
account2 = [10]
account3 = [20]
M = [account1[0] + account2[0] + account3[0]]
average = [int(M[0] / N0)]
# Remplissage des colonnes
for i in range(1, len(taxes_rel_accounts.index)):
# Taxes individuelles
taxe1 = get_taxe(c, account1[i-1])
taxe2 = get_taxe(c, account2[i-1])
taxe3 = get_taxe(c, account3[i-1])
# Montant collecté
collected = taxe1 + taxe2 + taxe3
# Nouveaux montants des comptes
redistribution1 = get_redistribution(c, N0, account1[i-1], taxe1, collected)
redistribution2 = get_redistribution(c, N0, account2[i-1], taxe2, collected)
redistribution3 = get_redistribution(c, N0, account3[i-1], taxe3, collected)
account1.append(redistribution1)
account2.append(redistribution2)
account3.append(redistribution3)
M.append(account1[i] + account2[i] + account3[i])
average.append(round(M[i] / N0))
# Affichage tableur
display(taxes_rel_accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | 3 | NaN |
| 2 | 2 | 1.000000 | 11.0 | 21.000000 | 33.0 | 3 | 11.0 |
| 3 | 3 | 1.909091 | 11.0 | 20.090909 | 33.0 | 3 | 11.0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 10.992852 | 11.0 | 11.007148 | 33.0 | 3 | 11.0 |
| 79 | 79 | 10.993502 | 11.0 | 11.006498 | 33.0 | 3 | 11.0 |
| 80 | 80 | 10.994093 | 11.0 | 11.005907 | 33.0 | 3 | 11.0 |
80 rows × 7 columns
Graphique en relatif par taxes¶
# Courbes sur le même graphique
ax = plt.gca()
taxes_rel_accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
taxes_rel_accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
taxes_rel_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
taxes_rel_accounts.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
plt.show()

Ici on constate qu’un système de redistribution par taxe produit le même effet de convergence des comptes que la création monétaire par un Dividende Universel.
On peut donc établir une équivalence entre un Revenu de Base financé par l’impôt (taxe) et le référentiel relatif au DU d’une monnaie libre.
Principe de parcimonie¶
Dans un système de taxe, on est jamais sûr d’obtenir l’impôt de toute la population (évasion fiscale, argent liquide non déclaré, etc). Dans la monnaie libre, la convergence des comptes est automatique sur toute la population utilisatrice et sans coercicion. Ainsi, selon le principe de parcimonie (le fameux rasoir d’okham), à forme équivalente, il est préférable d’utiliser une monnaie libre dont la simplicité de mise en oeuvre est bien supérieure aux moyens nécessités par la mise en place d’un revenu de base par l’impôt.
(b) Simuler des échanges entre I1 et I3¶
Echanges en quantitatif¶
# Echanges par année
exchanges12 = {
10: 20000,
30: -200000,
50: 1000000,
}
exchanges13 = {
20: 50000,
40: -200000,
60: 3000000,
}
# Nouveau tableur quantitatif avec échanges
exchanges_accounts = accounts.copy()
# Initialisation des colonnes
account1 = [0]
account2 = [account0]
account3 = [2 * account0]
M = [account1[0] + account2[0] + account3[0]]
N = [N0]
average = [int(M[0] / N[0])]
DU = [float('nan')]
full_average = [float('nan')]
# Remplissage des colonnes
for i in range(1, len(exchanges_accounts)):
N.append(N0)
new_DU = get_du(c, M, N, DU, i)
# Echanges
amount1 = 0
amount2 = 0
amount3 = 0
if i in exchanges12:
amount1 = exchanges12[i]
amount2 = -exchanges12[i]
if i in exchanges13:
amount1 = exchanges13[i]
amount3 = -exchanges13[i]
account1.append(account1[i-1] + new_DU + amount1)
account2.append(account2[i-1] + new_DU + amount2)
account3.append(account3[i-1] + new_DU + amount3)
M.append(account1[i] + account2[i] + account3[i])
DU.append(new_DU)
full_average.append(new_DU / c * (1 + c))
average.append(int(M[i] / N[i]))
# Remplissage du tableur
exchanges_accounts['I1'] = account1
exchanges_accounts['I2'] = account2
exchanges_accounts['I3'] = account3
exchanges_accounts['Masse Monétaire'] = M
exchanges_accounts['Moyenne'] = average
exchanges_accounts['DU'] = DU
# Affichage tableur
display(exchanges_accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.000000e+00 | 1.000000e+04 | 2.000000e+04 | 3.000000e+04 | 3 | 10000 | NaN | NaN |
| 2 | 2 | 1.000000e+03 | 1.100000e+04 | 2.100000e+04 | 3.300000e+04 | 3 | 11000 | 1.100000e+04 | 1.000000e+03 |
| 3 | 3 | 2.100000e+03 | 1.210000e+04 | 2.210000e+04 | 3.630000e+04 | 3 | 12100 | 1.210000e+04 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 1.904993e+07 | 1.456993e+07 | 1.254993e+07 | 4.616980e+07 | 3 | 15389933 | 1.538993e+07 | 1.399085e+06 |
| 79 | 79 | 2.058893e+07 | 1.610893e+07 | 1.408893e+07 | 5.078678e+07 | 3 | 16928927 | 1.692893e+07 | 1.538993e+06 |
| 80 | 80 | 2.228182e+07 | 1.780182e+07 | 1.578182e+07 | 5.586546e+07 | 3 | 18621820 | 1.862182e+07 | 1.692893e+06 |
80 rows × 9 columns
Graphique échanges en quantitatif (échelle logarithmique)¶
import matplotlib.pyplot as plt
# Courbes sur le même graphique
ax = plt.gca()
exchanges_accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
exchanges_accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
exchanges_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
exchanges_accounts.plot(kind='line', x='Année', y='Moyenne', style='--', color='black', ax=ax)
exchanges_accounts.plot(kind='line', x='Année', y='Moyenne', style='--', color='green', ax=ax)
# Echelle logarithmique de l'axe Y
plt.yscale("log")
plt.show()
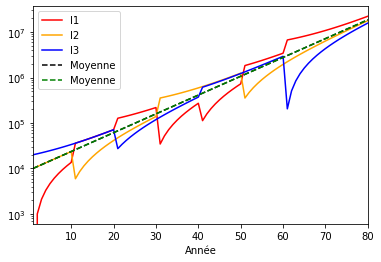
Lorsque les individus échanges, on s’aperçoit que cela ne perturbe en rien la symétrie spatiale de la création monétaire. Même si les montants des comptes diffèrent, il suivent la courbe de la moyenne.
Echanges en relatif¶
# Capture de la colonne DU
du_series = accounts['DU']
# Nouveau tableur relatif
exchanges_rel_accounts = exchanges_accounts.copy()
for label, series in exchanges_rel_accounts.items():
if label == 'Année' or label == 'N':
continue
exchanges_rel_accounts[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(exchanges_rel_accounts)
| Année | I1 | I2 | I3 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | 3 | NaN | NaN | NaN |
| 2 | 2 | 1.000000 | 11.000000 | 21.000000 | 33.0 | 3 | 11.000000 | 11.0 | 1.0 |
| 3 | 3 | 1.909091 | 11.000000 | 20.090909 | 33.0 | 3 | 11.000000 | 11.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 13.615996 | 10.413903 | 8.970102 | 33.0 | 3 | 10.999999 | 11.0 | 1.0 |
| 79 | 79 | 13.378178 | 10.467184 | 9.154638 | 33.0 | 3 | 11.000000 | 11.0 | 1.0 |
| 80 | 80 | 13.161980 | 10.515622 | 9.322398 | 33.0 | 3 | 11.000000 | 11.0 | 1.0 |
80 rows × 9 columns
Graphique échanges en relatif¶
# Courbes sur le même graphique
ax = plt.gca()
exchanges_rel_accounts.plot(kind='line', x='Année', y='I1', color='red', ax=ax)
exchanges_rel_accounts.plot(kind='line', x='Année', y='I2', color='orange', ax=ax)
exchanges_rel_accounts.plot(kind='line', x='Année', y='I3', color='blue', ax=ax)
exchanges_rel_accounts.plot(kind='line', x='Année', y='Moyenne', style='--', color='black', ax=ax)
exchanges_rel_accounts.plot(kind='line', x='Année', y='Moyenne Pleine', style='--', color='green', ax=ax)
plt.show()
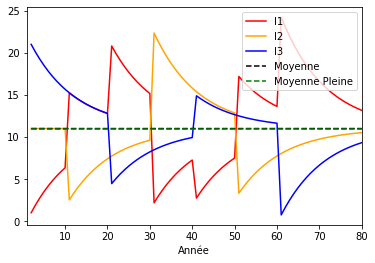
En relatif, même constat, les échanges s’effectuent et la convergence des comptes aussi. Les échanges ayant des montants identiques, ils apparaissent plus proche de la moyenne en fin de courbe, car ils sont plus faibles en rapport à la masse monétaire.
(c) Changements de référentiels dans le temps : remplacement générationnel¶
Réaliser un tableur Quantitatif avec I1, I2…, I10 d’âges 0 à 72 ans = 9 x 8 ans¶
# Initialisation des colonnes
years = [1]
accounts = list()
ages = list(range(0, ev, 8))
M = [0]
for index in range(0, len(ages)):
accounts.append([account0])
M[0] = M[0] + accounts[index][0]
N = [len(ages)]
average = [int(M[0] / N[0])]
DU = [float('nan')]
full_average = [float('nan')]
# Remplissage des colonnes
for i in range(1, ev):
years.append(years[i-1]+1)
current_N = 0
for index in range(0, len(ages)):
ages[index] += 1
if is_alive(ages[index]):
current_N += 1
N.append(current_N)
if current_N > 0:
new_DU = get_du(c, M, N, DU, i)
else:
new_DU = 0
current_M = 0
for index in range(0, len(ages)):
if is_alive(ages[index]):
accounts[index].append(accounts[index][i-1] + new_DU)
else:
accounts[index].append(accounts[index][i-1])
current_M += accounts[index][i]
M.append(current_M)
DU.append(new_DU)
full_average.append(new_DU / c * (1 + c))
average.append(int(current_M / current_N))
# Remplissage du tableur
accounts_in_time = pd.DataFrame(years, columns=['Année'], index=years)
for index in range(0, len(ages)):
accounts_in_time[f'I%d' % (index + 1)] = accounts[index]
accounts_in_time['Masse Monétaire'] = M
accounts_in_time['N'] = N
accounts_in_time['Moyenne'] = average
accounts_in_time['Moyenne Pleine'] = full_average
accounts_in_time['DU'] = DU
# Affichage tableur
display(accounts_in_time)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | I10 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000 | 1.000000e+05 | 10 | 10000 | NaN | NaN |
| 2 | 2 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 11000.000000 | 11000.000000 | 11000.000000 | 11000.000000 | 11000.000 | 1.100000e+05 | 10 | 11000 | 1.100000e+04 | 1.000000e+03 |
| 3 | 3 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 12100.000000 | 12100.000000 | 12100.000000 | 12100.000000 | 12100.000 | 1.210000e+05 | 10 | 12100 | 1.210000e+04 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 3.153240e+07 | 1.506433e+07 | 6.077581e+06 | 2.547684e+06 | 1.091849e+06 | 475079.389507 | 209262.772895 | 93308.024358 | 42234.775852 | 19487.171 | 5.715322e+07 | 1 | 57153216 | 4.259523e+07 | 3.872294e+06 |
| 79 | 79 | 3.593751e+07 | 1.506433e+07 | 6.077581e+06 | 2.547684e+06 | 1.091849e+06 | 475079.389507 | 209262.772895 | 93308.024358 | 42234.775852 | 19487.171 | 6.155832e+07 | 1 | 61558319 | 4.845613e+07 | 4.405103e+06 |
| 80 | 80 | 4.091414e+07 | 1.506433e+07 | 6.077581e+06 | 2.547684e+06 | 1.091849e+06 | 475079.389507 | 209262.772895 | 93308.024358 | 42234.775852 | 19487.171 | 6.653495e+07 | 1 | 66534954 | 5.474299e+07 | 4.976635e+06 |
80 rows × 16 columns
Graphique en quantitatif¶
# Courbes sur le même graphique
ax = plt.gca()
for index in range(0, len(ages)):
accounts_in_time.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
accounts_in_time.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
accounts_in_time.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
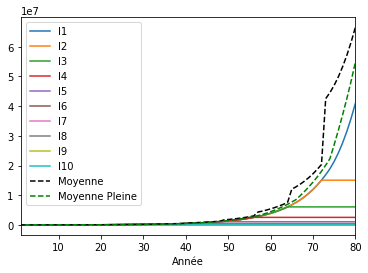
Sur ce graphique, les utilisateurs naissent décalés dans le temps. On constate qu’à leur décès, ils laissent une somme fixe qui subsiste dans la masse monétaire, mais représente une proportion moindre au fil du temps car la masse monétaire continue à augmenter grâce aux dividendes créés par les vivants.
La moyenne (M/N), comme on pouvait s’y attendre, est modifiée par la fluctuation de N. Mais poursuit une trajectoire exponentielle. Les vivants voient leurs comptes suivrent une courbe exponentielle régulière malgré les irrégularités de la moyenne.
Referentiel en quantitatif à somme nulle¶
# Capture de la colonne Moyenne
average_series = accounts_in_time['Moyenne']
# Nouveau tableur quantitatif à somme nulle
sum_zero_accounts_in_time = accounts_in_time.copy()
sum_zero_accounts_in_time['Masse Monétaire'] = 0
for label, series in sum_zero_accounts_in_time.items():
if label.startswith('I'):
sum_zero_accounts_in_time[label] = series.sub(average_series).astype('float64')
sum_zero_accounts_in_time['Masse Monétaire'] = sum_zero_accounts_in_time['Masse Monétaire'] + sum_zero_accounts_in_time[label]
sum_zero_accounts_in_time['Moyenne Pleine'] = sum_zero_accounts_in_time['Moyenne Pleine'].sub(average_series).astype('float64')
sum_zero_accounts_in_time['Moyenne'] = sum_zero_accounts_in_time['Masse Monétaire'] / sum_zero_accounts_in_time['N']
# Affichage tableur
display(sum_zero_accounts_in_time)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | I10 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 10 | 0.000000e+00 | NaN | NaN |
| 2 | 2 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 10 | 0.000000e+00 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 10 | 0.000000e+00 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | -2.562081e+07 | -4.208889e+07 | -5.107564e+07 | -5.460553e+07 | -5.606137e+07 | -5.667814e+07 | -5.694395e+07 | -5.705991e+07 | -5.711098e+07 | -5.713373e+07 | -5.143789e+08 | 1 | -5.143789e+08 | -1.455799e+07 | 3.872294e+06 |
| 79 | 79 | -2.562081e+07 | -4.649399e+07 | -5.548074e+07 | -5.901064e+07 | -6.046647e+07 | -6.108324e+07 | -6.134906e+07 | -6.146501e+07 | -6.151608e+07 | -6.153883e+07 | -5.540249e+08 | 1 | -5.540249e+08 | -1.310219e+07 | 4.405103e+06 |
| 80 | 80 | -2.562081e+07 | -5.147063e+07 | -6.045737e+07 | -6.398727e+07 | -6.544310e+07 | -6.605987e+07 | -6.632569e+07 | -6.644165e+07 | -6.649272e+07 | -6.651547e+07 | -5.988146e+08 | 1 | -5.988146e+08 | -1.179197e+07 | 4.976635e+06 |
80 rows × 16 columns
Graphique en quantitatif à somme nulle¶
# Courbes sur le même graphique
ax = plt.gca()
for index in range(0, len(ages)):
sum_zero_accounts_in_time.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
sum_zero_accounts_in_time.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_accounts_in_time.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
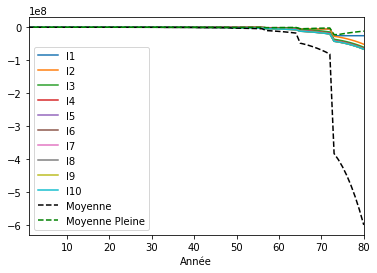
Contrairement au graphique quantitatif à somme nulle précédent où les comptes maintenait leur montant au cours de leur vie, ici les morts et les vivants voient leur comptes chuter par rapport à la moyenne. C’est normal puisque la moyenne augmente après chaque décès.
Référentiel relatif¶
# Capture de la colonne DU
du_series = accounts_in_time['DU']
# Nouveau tableur relatif
rel_accounts_in_time = accounts_in_time.copy()
for label, series in rel_accounts_in_time.items():
if label == 'Année' or label == 'N':
continue
rel_accounts_in_time[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(rel_accounts_in_time)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | I10 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 10 | NaN | NaN | NaN |
| 2 | 2 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 110.000000 | 10 | 11.000000 | 11.0 | 1.0 |
| 3 | 3 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 110.000000 | 10 | 11.000000 | 11.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 8.143082 | 3.890285 | 1.569504 | 0.657926 | 0.281964 | 0.122687 | 0.054041 | 0.024096 | 0.010907 | 0.005032 | 14.759526 | 1 | 14.759525 | 11.0 | 1.0 |
| 79 | 79 | 8.158154 | 3.419744 | 1.379668 | 0.578348 | 0.247860 | 0.107848 | 0.047505 | 0.021182 | 0.009588 | 0.004424 | 13.974321 | 1 | 13.974320 | 11.0 | 1.0 |
| 80 | 80 | 8.221246 | 3.027010 | 1.221223 | 0.511929 | 0.219395 | 0.095462 | 0.042049 | 0.018749 | 0.008487 | 0.003916 | 13.369466 | 1 | 13.369466 | 11.0 | 1.0 |
80 rows × 16 columns
Graphique en relatif¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(10,6))
for index in range(0, len(ages)):
rel_accounts_in_time.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
rel_accounts_in_time.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
rel_accounts_in_time.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
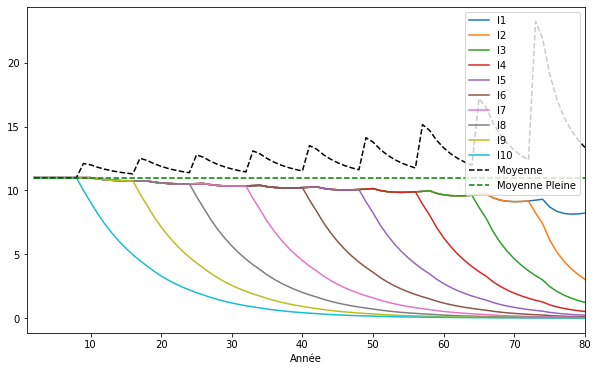
En relatif, les comptes des morts descendent vers zéro. La monnaie des morts disparaît, elle est détruite !
Ainsi, elle laisse la place à celle des vivants. Observez également comment la moyenne est perturbée, mais converge toujours inéxorablement vers 11 DU, comme un ressort…
Référentiel relatif à somme nulle¶
# Capture de la colonne DU
du_series = rel_accounts_in_time['DU']
# Nouveau tableur relatif à somme nulle
sum_zero_rel_accounts_in_time = sum_zero_accounts_in_time.copy()
for label, series in sum_zero_rel_accounts_in_time.items():
if label == 'Année' or label == 'N':
continue
sum_zero_rel_accounts_in_time[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(sum_zero_rel_accounts_in_time)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | I10 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 10 | NaN | NaN | NaN |
| 2 | 2 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 10 | 0.000000e+00 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 10 | 0.000000e+00 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | -2.562081e+07 | -4.208889e+07 | -5.107564e+07 | -5.460553e+07 | -5.606137e+07 | -5.667814e+07 | -5.694395e+07 | -5.705991e+07 | -5.711098e+07 | -5.713373e+07 | -5.143789e+08 | 1 | -5.143789e+08 | -1.455799e+07 | 3.872294e+06 |
| 79 | 79 | -2.562081e+07 | -4.649399e+07 | -5.548074e+07 | -5.901064e+07 | -6.046647e+07 | -6.108324e+07 | -6.134906e+07 | -6.146501e+07 | -6.151608e+07 | -6.153883e+07 | -5.540249e+08 | 1 | -5.540249e+08 | -1.310219e+07 | 4.405103e+06 |
| 80 | 80 | -2.562081e+07 | -5.147063e+07 | -6.045737e+07 | -6.398727e+07 | -6.544310e+07 | -6.605987e+07 | -6.632569e+07 | -6.644165e+07 | -6.649272e+07 | -6.651547e+07 | -5.988146e+08 | 1 | -5.988146e+08 | -1.179197e+07 | 4.976635e+06 |
80 rows × 16 columns
Graphique en relatif à somme nulle¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(10,6))
for index in range(0, len(ages)):
sum_zero_rel_accounts_in_time.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
sum_zero_rel_accounts_in_time.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_rel_accounts_in_time.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
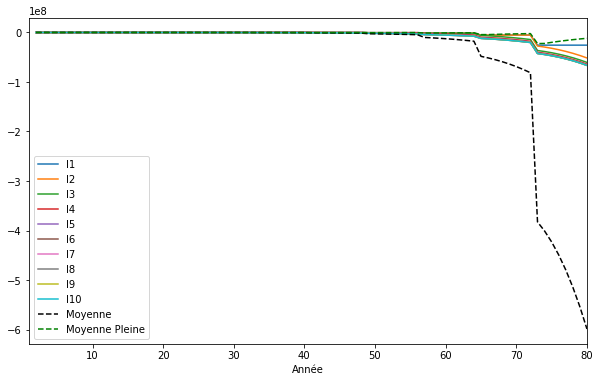
Ici les décès entraînent des sautes vers le haut de la moyenne, faisant descendre abruptement les comptes par rapport à cette moyenne. Mais le Dividende Universel les ramène à la moyenne jusqu’au prochain décès.
Rajouter I11, I12…, I20 qui seront les nouveaux entrants successifs aux dates idoines¶
# Initialisation des colonnes
years = [1]
accounts = list()
ages = list(range(0, ev, 8)) + list(range(-ev, 0, 8))
M = [0]
N = [0]
for index in range(0, len(ages)):
accounts.append([0])
if is_alive(ages[index]):
accounts[index][0] = account0
M[0] = M[0] + accounts[index][0]
N[0] = N[0] + 1
average = [int(M[0] / N[0])]
DU = [float('nan')]
full_average = [float('nan')]
# Remplissage des colonnes
for i in range(1, ev):
years.append(years[i-1]+1)
current_N = 0
for index in range(0, len(ages)):
ages[index] += 1
if is_alive(ages[index]):
current_N += 1
N.append(current_N)
if current_N > 0:
new_DU = get_du(c, M, N, DU, i)
else:
new_DU = 0
current_M = 0
for index in range(0, len(ages)):
if is_alive(ages[index]):
accounts[index].append(accounts[index][i-1] + new_DU)
else:
accounts[index].append(accounts[index][i-1])
current_M += accounts[index][i]
M.append(current_M)
DU.append(new_DU)
full_average.append(new_DU / c * (1 + c))
average.append(int(current_M / current_N))
# Remplissage du tableur
accounts_in_time_20 = pd.DataFrame(years, columns=['Année'], index=years)
for index in range(0, len(ages)):
accounts_in_time_20[f'I%d' % (index + 1)] = accounts[index]
accounts_in_time_20['Masse Monétaire'] = M
accounts_in_time_20['N'] = N
accounts_in_time_20['Moyenne'] = average
accounts_in_time_20['Moyenne Pleine'] = full_average
accounts_in_time_20['DU'] = DU
# Affichage tableur
display(accounts_in_time_20)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I16 | I17 | I18 | I19 | I20 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 10000.00000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | ... | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.000000e+05 | 10 | 10000 | NaN | NaN |
| 2 | 2 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 11000.00000 | 11000.000000 | 11000.000000 | 11000.000000 | 11000.000000 | ... | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.100000e+05 | 10 | 11000 | 1.100000e+04 | 1.000000e+03 |
| 3 | 3 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 12100.00000 | 12100.000000 | 12100.000000 | 12100.000000 | 12100.000000 | ... | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.210000e+05 | 10 | 12100 | 1.210000e+04 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 1.538993e+07 | 8.687217e+06 | 4.052651e+06 | 1.890591e+06 | 881974.85259 | 411447.777893 | 191943.424958 | 89543.024326 | 41772.481694 | ... | 1.497849e+07 | 1.519799e+07 | 1.530039e+07 | 1.534816e+07 | 1.537045e+07 | 1.538993e+08 | 10 | 15389933 | 1.538993e+07 | 1.399085e+06 |
| 79 | 79 | 1.692893e+07 | 8.687217e+06 | 4.052651e+06 | 1.890591e+06 | 881974.85259 | 411447.777893 | 191943.424958 | 89543.024326 | 41772.481694 | ... | 1.651748e+07 | 1.673698e+07 | 1.683938e+07 | 1.688715e+07 | 1.690944e+07 | 1.692893e+08 | 10 | 16928927 | 1.692893e+07 | 1.538993e+06 |
| 80 | 80 | 1.862182e+07 | 8.687217e+06 | 4.052651e+06 | 1.890591e+06 | 881974.85259 | 411447.777893 | 191943.424958 | 89543.024326 | 41772.481694 | ... | 1.821037e+07 | 1.842988e+07 | 1.853228e+07 | 1.858005e+07 | 1.860233e+07 | 1.862182e+08 | 10 | 18621820 | 1.862182e+07 | 1.692893e+06 |
80 rows × 26 columns
Graphique en quantitatif¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(10,6))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 2:
accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
else:
accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.legend(loc='upper left')
plt.show()
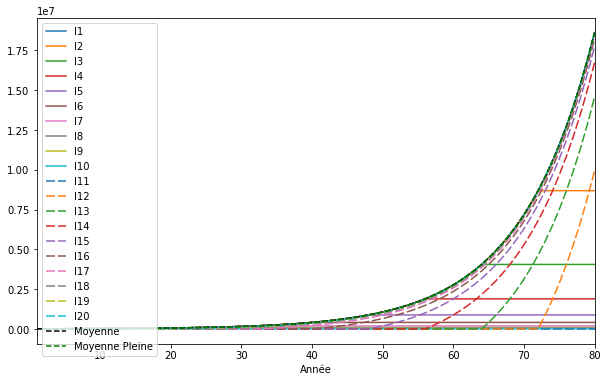
Lorsqu’un mort est immédiatement remplacé par un nouveau né, la moyenne n’est plus perturbée, puisque N est à nouveau constant.
Ici pas de changement sur le comportement en quantitatif par rapport aux trois comptes. On observe toujours une convergence vers la moyenne même pour les nouveaux arrivants (en pointillé).
Referentiel en quantitatif à somme nulle¶
# Capture de la colonne Moyenne
average_series = accounts_in_time_20['Moyenne']
# Nouveau tableur quantitatif à somme nulle
sum_zero_accounts_in_time_20 = accounts_in_time_20.copy()
sum_zero_accounts_in_time_20['Masse Monétaire'] = 0
for label, series in sum_zero_accounts_in_time_20.items():
if label.startswith('I'):
sum_zero_accounts_in_time_20[label] = series.sub(average_series).astype('float64')
sum_zero_accounts_in_time_20['Masse Monétaire'] = sum_zero_accounts_in_time_20['Masse Monétaire'] + sum_zero_accounts_in_time_20[label]
sum_zero_accounts_in_time_20['Moyenne Pleine'] = sum_zero_accounts_in_time_20['Moyenne Pleine'].sub(average_series).astype('float64')
sum_zero_accounts_in_time_20['Moyenne'] = sum_zero_accounts_in_time_20['Masse Monétaire'] / sum_zero_accounts_in_time_20['N']
# Affichage tableur
display(sum_zero_accounts_in_time_20)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I16 | I17 | I18 | I19 | I20 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -10000.000000 | -10000.000000 | -10000.000000 | -10000.000000 | -10000.000000 | -1.000000e+05 | 10 | -1.000000e+04 | NaN | NaN |
| 2 | 2 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -11000.000000 | -11000.000000 | -11000.000000 | -11000.000000 | -11000.000000 | -1.100000e+05 | 10 | -1.100000e+04 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -12100.000000 | -12100.000000 | -12100.000000 | -12100.000000 | -12100.000000 | -1.210000e+05 | 10 | -1.210000e+04 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 0.993880 | -6.702716e+06 | -1.133728e+07 | -1.349934e+07 | -1.450796e+07 | -1.497849e+07 | -1.519799e+07 | -1.530039e+07 | -1.534816e+07 | ... | -411446.784012 | -191942.431077 | -89542.030445 | -41771.487814 | -19486.177120 | -1.538993e+08 | 10 | -1.538993e+07 | 9.938803e-01 | 1.399085e+06 |
| 79 | 79 | 0.393268 | -8.241710e+06 | -1.287628e+07 | -1.503834e+07 | -1.604695e+07 | -1.651748e+07 | -1.673698e+07 | -1.683938e+07 | -1.688715e+07 | ... | -411447.384624 | -191943.031689 | -89542.631057 | -41772.088426 | -19486.777732 | -1.692893e+08 | 10 | -1.692893e+07 | 3.932683e-01 | 1.538993e+06 |
| 80 | 80 | 0.132595 | -9.934603e+06 | -1.456917e+07 | -1.673123e+07 | -1.773985e+07 | -1.821037e+07 | -1.842988e+07 | -1.853228e+07 | -1.858005e+07 | ... | -411447.645297 | -191943.292363 | -89542.891730 | -41772.349099 | -19487.038405 | -1.862182e+08 | 10 | -1.862182e+07 | 1.325952e-01 | 1.692893e+06 |
80 rows × 26 columns
Graphique en quantitatif à somme nulle¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(10,6))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 2:
sum_zero_accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
else:
sum_zero_accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
sum_zero_accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.legend(loc='upper left')
plt.show()
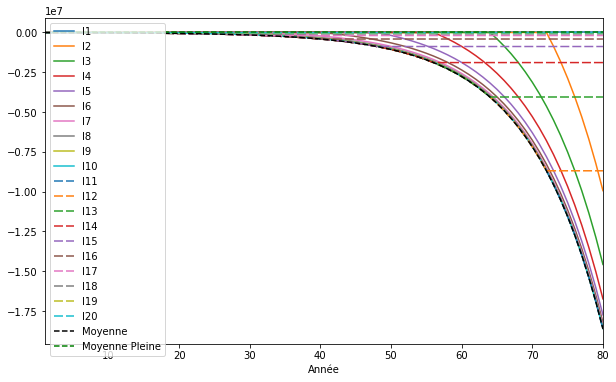
Dans ce référentiel, on constate que les morts descendent toujours dans les abîmes du négatifs, alors que les nouveaux arrivants ont des comptes stables de leur vivant, par rapport à la moyenne.
Référentiel relatif¶
# Capture de la colonne DU
du_series = accounts_in_time_20['DU']
# Nouveau tableur relatif
rel_accounts_in_time_20 = accounts_in_time_20.copy()
for label, series in rel_accounts_in_time_20.items():
if label == 'Année' or label == 'N':
continue
rel_accounts_in_time_20[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(rel_accounts_in_time_20)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I16 | I17 | I18 | I19 | I20 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | 10 | NaN | NaN | NaN |
| 2 | 2 | 11.0 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 110.0 | 10 | 11.000000 | 11.0 | 1.0 |
| 3 | 3 | 11.0 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 110.0 | 10 | 11.000000 | 11.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 11.0 | 6.209213 | 2.896644 | 1.351306 | 0.630394 | 0.294083 | 0.137192 | 0.064001 | 0.029857 | ... | 10.705917 | 10.862808 | 10.935999 | 10.970143 | 10.986071 | 110.0 | 10 | 10.999999 | 11.0 | 1.0 |
| 79 | 79 | 11.0 | 5.644739 | 2.633313 | 1.228460 | 0.573086 | 0.267349 | 0.124720 | 0.058183 | 0.027143 | ... | 10.732651 | 10.875280 | 10.941817 | 10.972857 | 10.987338 | 110.0 | 10 | 11.000000 | 11.0 | 1.0 |
| 80 | 80 | 11.0 | 5.131581 | 2.393920 | 1.116782 | 0.520987 | 0.243044 | 0.113382 | 0.052894 | 0.024675 | ... | 10.756956 | 10.886618 | 10.947106 | 10.975325 | 10.988489 | 110.0 | 10 | 11.000000 | 11.0 | 1.0 |
80 rows × 26 columns
Graphique en relatif¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(10,6))
ages = list(range(0, ev, 8)) + list(range(-ev, 0, 8))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 2:
rel_accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
else:
rel_accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
rel_accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
rel_accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.legend(loc='best')
plt.show()
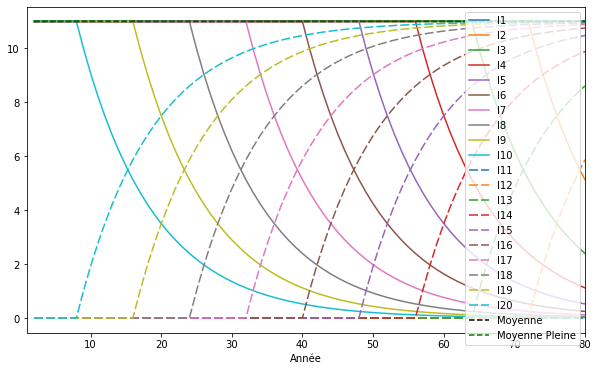
Dans le référentiel relatif, le renouvellement des générations ne change rien à la convergence des nouveaux arrivants vers la moyenne et à la chute vers zéro de la monnaie des morts.
Par contre, la stabilité de N étant rétablie, la moyenne est à nouveau stable.
On constate que chaque individu, quelque soit le moment de son arrivée, converge vers la moyenne sur la même durée (environ 40 ans). On a donc une vraie symétrie temporelle car cela signifie que chaque individu crée le même nombre de Dividendes Universels pendant cette durée.
Référentiel relatif à somme nulle¶
# Capture de la colonne Moyenne
du_series = rel_accounts_in_time_20['DU']
# Nouveau tableur relatif à somme nulle
sum_zero_rel_accounts_in_time_20 = sum_zero_accounts_in_time_20.copy()
for label, series in sum_zero_rel_accounts_in_time_20.items():
if label == 'Année' or label == 'N':
continue
sum_zero_rel_accounts_in_time_20[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(sum_zero_rel_accounts_in_time_20)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I16 | I17 | I18 | I19 | I20 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | 10 | NaN | NaN | NaN |
| 2 | 2 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -11000.000000 | -11000.000000 | -11000.000000 | -11000.000000 | -11000.000000 | -1.100000e+05 | 10 | -1.100000e+04 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | 0.000000 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -12100.000000 | -12100.000000 | -12100.000000 | -12100.000000 | -12100.000000 | -1.210000e+05 | 10 | -1.210000e+04 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 78 | 78 | 0.993880 | -6.702716e+06 | -1.133728e+07 | -1.349934e+07 | -1.450796e+07 | -1.497849e+07 | -1.519799e+07 | -1.530039e+07 | -1.534816e+07 | ... | -411446.784012 | -191942.431077 | -89542.030445 | -41771.487814 | -19486.177120 | -1.538993e+08 | 10 | -1.538993e+07 | 9.938803e-01 | 1.399085e+06 |
| 79 | 79 | 0.393268 | -8.241710e+06 | -1.287628e+07 | -1.503834e+07 | -1.604695e+07 | -1.651748e+07 | -1.673698e+07 | -1.683938e+07 | -1.688715e+07 | ... | -411447.384624 | -191943.031689 | -89542.631057 | -41772.088426 | -19486.777732 | -1.692893e+08 | 10 | -1.692893e+07 | 3.932683e-01 | 1.538993e+06 |
| 80 | 80 | 0.132595 | -9.934603e+06 | -1.456917e+07 | -1.673123e+07 | -1.773985e+07 | -1.821037e+07 | -1.842988e+07 | -1.853228e+07 | -1.858005e+07 | ... | -411447.645297 | -191943.292363 | -89542.891730 | -41772.349099 | -19487.038405 | -1.862182e+08 | 10 | -1.862182e+07 | 1.325952e-01 | 1.692893e+06 |
80 rows × 26 columns
Graphique en relatif à somme nulle¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(10,6))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 2:
sum_zero_rel_accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
else:
sum_zero_rel_accounts_in_time_20.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
sum_zero_rel_accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_rel_accounts_in_time_20.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.legend(loc='upper left')
plt.show()
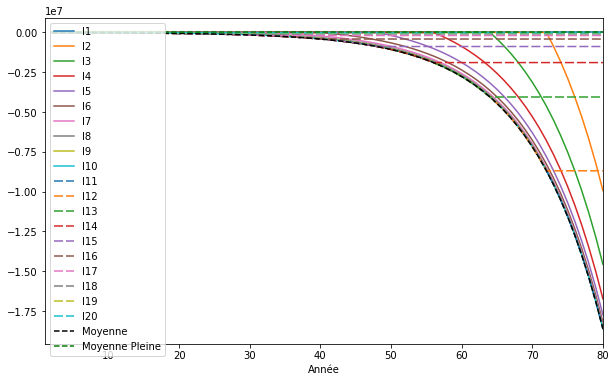
Comme dans le référentiel relatif, les vivants convergent vers la moyenne et les morts tombent dans les abysses du négatif…
Pousser les données à 160 ans, les I10+k étant remplacés par des I20+k¶
# Initialisation des colonnes
years = [1]
accounts = list()
ages = list(range(0, ev, 8)) + list(range(-ev, 0, 8)) + list(range(-2*ev, -ev, 8))
M = [0]
N = [0]
for index in range(0, len(ages)):
accounts.append([0])
if is_alive(ages[index]):
accounts[index][0] = account0
M[0] = M[0] + accounts[index][0]
N[0] = N[0] + 1
average = [int(M[0] / N[0])]
DU = [float('nan')]
full_average = [float('nan')]
# Remplissage des colonnes
for i in range(1, ev*2):
years.append(years[i-1]+1)
current_N = 0
for index in range(0, len(ages)):
ages[index] += 1
if is_alive(ages[index]):
current_N += 1
N.append(current_N)
if current_N > 0:
new_DU = get_du(c, M, N, DU, i)
else:
new_DU = 0
current_M = 0
for index in range(0, len(ages)):
if is_alive(ages[index]):
accounts[index].append(accounts[index][i-1] + new_DU)
else:
accounts[index].append(accounts[index][i-1])
current_M += accounts[index][i]
M.append(current_M)
DU.append(new_DU)
full_average.append(new_DU / c * (1 + c))
average.append(int(current_M / current_N))
# Remplissage du tableur
accounts_in_time_160 = pd.DataFrame(years, columns=['Année'], index=years)
for index in range(0, len(ages)):
accounts_in_time_160[f'I%d' % (index + 1)] = accounts[index]
accounts_in_time_160['Masse Monétaire'] = M
accounts_in_time_160['N'] = N
accounts_in_time_160['Moyenne'] = average
accounts_in_time_160['Moyenne Pleine'] = full_average
accounts_in_time_160['DU'] = DU
# Affichage tableur
display(accounts_in_time_160)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I26 | I27 | I28 | I29 | I30 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 1.000000e+04 | 10000.00000 | 10000.000000 | 10000.000000 | 10000.000000 | 10000.000000 | ... | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.000000e+05 | 10 | 10000 | NaN | NaN |
| 2 | 2 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 1.100000e+04 | 11000.00000 | 11000.000000 | 11000.000000 | 11000.000000 | 11000.000000 | ... | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.100000e+05 | 10 | 11000 | 1.100000e+04 | 1.000000e+03 |
| 3 | 3 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 1.210000e+04 | 12100.00000 | 12100.000000 | 12100.000000 | 12100.000000 | 12100.000000 | ... | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.210000e+05 | 10 | 12100 | 1.210000e+04 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 158 | 158 | 1.862182e+07 | 8.687217e+06 | 4.052651e+06 | 1.890591e+06 | 881974.85259 | 411447.777893 | 191943.424958 | 89543.024326 | 41772.481694 | ... | 3.068193e+10 | 3.113157e+10 | 3.134132e+10 | 3.143918e+10 | 3.148483e+10 | 3.152474e+11 | 10 | 31524744095 | 3.152474e+10 | 2.865886e+09 |
| 159 | 159 | 1.862182e+07 | 8.687217e+06 | 4.052651e+06 | 1.890591e+06 | 881974.85259 | 411447.777893 | 191943.424958 | 89543.024326 | 41772.481694 | ... | 3.383441e+10 | 3.428404e+10 | 3.449380e+10 | 3.459165e+10 | 3.463730e+10 | 3.467722e+11 | 10 | 34677218505 | 3.467722e+10 | 3.152474e+09 |
| 160 | 160 | 1.862182e+07 | 8.687217e+06 | 4.052651e+06 | 1.890591e+06 | 881974.85259 | 411447.777893 | 191943.424958 | 89543.024326 | 41772.481694 | ... | 3.730213e+10 | 3.775176e+10 | 3.796152e+10 | 3.805937e+10 | 3.810502e+10 | 3.814494e+11 | 10 | 38144940355 | 3.814494e+10 | 3.467722e+09 |
160 rows × 36 columns
Graphique en quantitatif¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(20,10))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 3:
accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
elif index >= (len(ages) / 3) and (index < (len(ages) / 3) * 2):
accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
else:
accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[2, 2], ax=ax)
accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.show()
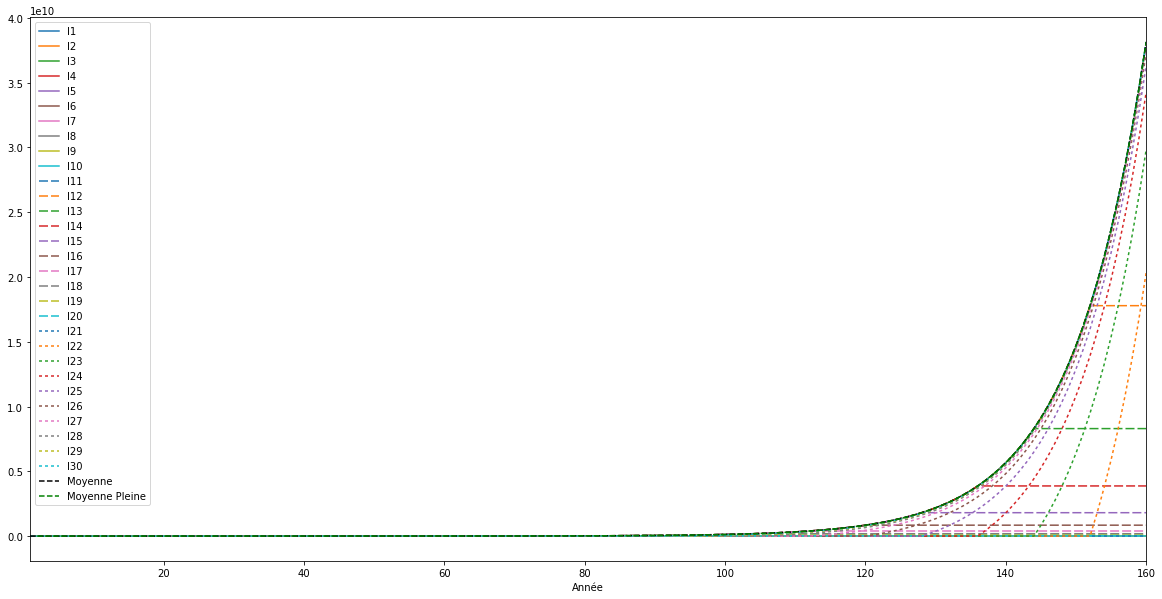
A la fin des 160 ans, on constate le même graphique qu’à la fin des 80 ans lorsque les vivants remplace les morts. C’est une bonne nouvelle, le fonctionnement de la monnaie libre reste constant au cours des générations et ne s’effondre pas.
Les morts de la seconde génération conservent des comptes à montant fixe (pointillé large) et les nouveaux arrivants de la troisième génération convergent vers la moyenne (pointillé court).
Referentiel en quantitatif à somme nulle¶
# Capture de la colonne Moyenne
average_series = accounts_in_time_160['Moyenne']
# Nouveau tableur quantitatif à somme nulle
sum_zero_accounts_in_time_160 = accounts_in_time_160.copy()
sum_zero_accounts_in_time_160['Masse Monétaire'] = 0
for label, series in sum_zero_accounts_in_time_160.items():
if label.startswith('I'):
sum_zero_accounts_in_time_160[label] = series.sub(average_series).astype('float64')
sum_zero_accounts_in_time_160['Masse Monétaire'] = sum_zero_accounts_in_time_160['Masse Monétaire'] + sum_zero_accounts_in_time_160[label]
sum_zero_accounts_in_time_160['Moyenne Pleine'] = sum_zero_accounts_in_time_160['Moyenne Pleine'].sub(average_series).astype('float64')
sum_zero_accounts_in_time_160['Moyenne'] = sum_zero_accounts_in_time_160['Masse Monétaire'] / sum_zero_accounts_in_time_160['N']
# Affichage tableur
display(sum_zero_accounts_in_time_160)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I26 | I27 | I28 | I29 | I30 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -1.000000e+04 | -1.000000e+04 | -1.000000e+04 | -1.000000e+04 | -1.000000e+04 | -2.000000e+05 | 10 | -2.000000e+04 | NaN | NaN |
| 2 | 2 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -1.100000e+04 | -1.100000e+04 | -1.100000e+04 | -1.100000e+04 | -1.100000e+04 | -2.200000e+05 | 10 | -2.200000e+04 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -1.210000e+04 | -1.210000e+04 | -1.210000e+04 | -1.210000e+04 | -1.210000e+04 | -2.420000e+05 | 10 | -2.420000e+04 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 158 | 158 | -3.150612e+10 | -3.151606e+10 | -3.152069e+10 | -3.152285e+10 | -3.152386e+10 | -3.152433e+10 | -3.152455e+10 | -3.152465e+10 | -3.152470e+10 | ... | -8.428097e+08 | -3.931770e+08 | -1.834199e+08 | -8.556676e+07 | -3.991752e+07 | -6.304949e+11 | 10 | -6.304949e+10 | 5.205612e-01 | 2.865886e+09 |
| 159 | 159 | -3.465860e+10 | -3.466853e+10 | -3.467317e+10 | -3.467533e+10 | -3.467634e+10 | -3.467681e+10 | -3.467703e+10 | -3.467713e+10 | -3.467718e+10 | ... | -8.428097e+08 | -3.931770e+08 | -1.834200e+08 | -8.556676e+07 | -3.991753e+07 | -6.935444e+11 | 10 | -6.935444e+10 | 7.261658e-02 | 3.152474e+09 |
| 160 | 160 | -3.812632e+10 | -3.813625e+10 | -3.814089e+10 | -3.814305e+10 | -3.814406e+10 | -3.814453e+10 | -3.814475e+10 | -3.814485e+10 | -3.814490e+10 | ... | -8.428097e+08 | -3.931770e+08 | -1.834199e+08 | -8.556676e+07 | -3.991752e+07 | -7.628988e+11 | 10 | -7.628988e+10 | 5.798721e-01 | 3.467722e+09 |
160 rows × 36 columns
Graphique en quantitatif à somme nulle¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(20,10))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 3:
sum_zero_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
elif index >= (len(ages) / 3) and (index < (len(ages) / 3) * 2):
sum_zero_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
else:
sum_zero_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[2, 2], ax=ax)
sum_zero_accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
sum_zero_accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.legend(loc='upper left')
plt.show()

Ici même constat, et la moyenne est stable comme ailleurs grâce au renouvellement des générations.
Référentiel relatif¶
# Capture de la colonne DU
du_series = accounts_in_time_160['DU']
# Nouveau tableur relatif
rel_accounts_in_time_160 = accounts_in_time_160.copy()
for label, series in rel_accounts_in_time_160.items():
if label == 'Année' or label == 'N':
continue
rel_accounts_in_time_160[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(rel_accounts_in_time_160)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I26 | I27 | I28 | I29 | I30 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | 10 | NaN | NaN | NaN |
| 2 | 2 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 110.0 | 10 | 11.0 | 11.0 | 1.0 |
| 3 | 3 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | 11.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 110.0 | 10 | 11.0 | 11.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 158 | 158 | 0.006498 | 0.003031 | 0.001414 | 0.000660 | 0.000308 | 0.000144 | 0.000067 | 0.000031 | 0.000015 | ... | 10.705917 | 10.862808 | 10.935999 | 10.970143 | 10.986071 | 110.0 | 10 | 11.0 | 11.0 | 1.0 |
| 159 | 159 | 0.005907 | 0.002756 | 0.001286 | 0.000600 | 0.000280 | 0.000131 | 0.000061 | 0.000028 | 0.000013 | ... | 10.732651 | 10.875280 | 10.941817 | 10.972857 | 10.987338 | 110.0 | 10 | 11.0 | 11.0 | 1.0 |
| 160 | 160 | 0.005370 | 0.002505 | 0.001169 | 0.000545 | 0.000254 | 0.000119 | 0.000055 | 0.000026 | 0.000012 | ... | 10.756956 | 10.886618 | 10.947106 | 10.975325 | 10.988489 | 110.0 | 10 | 11.0 | 11.0 | 1.0 |
160 rows × 36 columns
Graphique en relatif¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(20,10))
ages = list(range(0, ev, 8)) + list(range(-ev, 0, 8)) + list(range(-2*ev, -80, 8))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 3:
rel_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
elif index >= (len(ages) / 3) and (index < (len(ages) / 3) * 2):
rel_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
else:
rel_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[2, 2], ax=ax)
rel_accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne', color='black', style='--', ax=ax)
rel_accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne Pleine', color='green', style='--', ax=ax)
plt.legend(loc='upper left')
plt.show()
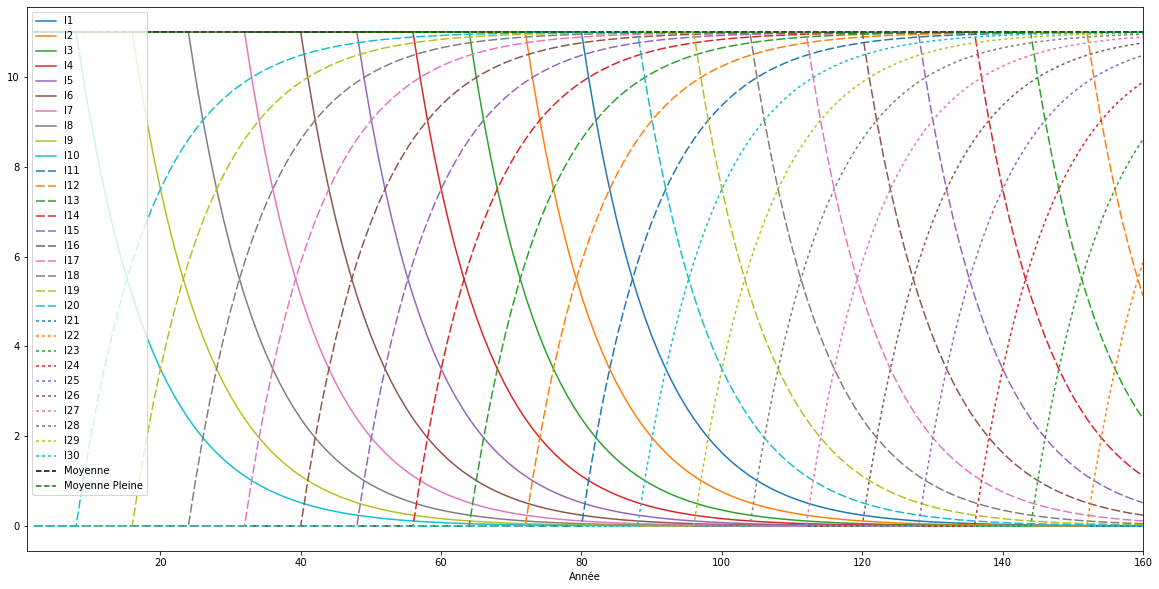
En relatif, on observe mieux le renouvellement des générations qui se poursuit sur l’espérance de vie de deux genérations.
La monnaie des morts disparaît et la monnaie des vivants converge vers la moyenne même sur 160 ans.
La symétrie temporelle perdure toujours de générations en générations… Un système pérenne donc.
Référentiel relatif à somme nulle¶
# Capture de la colonne DU
du_series = rel_accounts_in_time_160['DU']
# Nouveau tableur relatif à somme nulle
sum_zero_rel_accounts_in_time_160 = sum_zero_accounts_in_time_160.copy()
for label, series in sum_zero_rel_accounts_in_time_160.items():
if label == 'Année' or label == 'N':
continue
sum_zero_rel_accounts_in_time_160[label] = series.div(du_series).astype('float64')
# Affichage tableur
display(sum_zero_rel_accounts_in_time_160)
| Année | I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | ... | I26 | I27 | I28 | I29 | I30 | Masse Monétaire | N | Moyenne | Moyenne Pleine | DU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | 10 | NaN | NaN | NaN |
| 2 | 2 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -1.100000e+04 | -1.100000e+04 | -1.100000e+04 | -1.100000e+04 | -1.100000e+04 | -2.200000e+05 | 10 | -2.200000e+04 | 0.000000e+00 | 1.000000e+03 |
| 3 | 3 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | ... | -1.210000e+04 | -1.210000e+04 | -1.210000e+04 | -1.210000e+04 | -1.210000e+04 | -2.420000e+05 | 10 | -2.420000e+04 | 1.818989e-12 | 1.100000e+03 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 158 | 158 | -3.150612e+10 | -3.151606e+10 | -3.152069e+10 | -3.152285e+10 | -3.152386e+10 | -3.152433e+10 | -3.152455e+10 | -3.152465e+10 | -3.152470e+10 | ... | -8.428097e+08 | -3.931770e+08 | -1.834199e+08 | -8.556676e+07 | -3.991752e+07 | -6.304949e+11 | 10 | -6.304949e+10 | 5.205612e-01 | 2.865886e+09 |
| 159 | 159 | -3.465860e+10 | -3.466853e+10 | -3.467317e+10 | -3.467533e+10 | -3.467634e+10 | -3.467681e+10 | -3.467703e+10 | -3.467713e+10 | -3.467718e+10 | ... | -8.428097e+08 | -3.931770e+08 | -1.834200e+08 | -8.556676e+07 | -3.991753e+07 | -6.935444e+11 | 10 | -6.935444e+10 | 7.261658e-02 | 3.152474e+09 |
| 160 | 160 | -3.812632e+10 | -3.813625e+10 | -3.814089e+10 | -3.814305e+10 | -3.814406e+10 | -3.814453e+10 | -3.814475e+10 | -3.814485e+10 | -3.814490e+10 | ... | -8.428097e+08 | -3.931770e+08 | -1.834199e+08 | -8.556676e+07 | -3.991752e+07 | -7.628988e+11 | 10 | -7.628988e+10 | 5.798721e-01 | 3.467722e+09 |
160 rows × 36 columns
Graphique en relatif à somme nulle¶
# Courbes sur le même graphique
fig, ax = plt.subplots(1, 1, figsize=(20,10))
ages = list(range(0, ev, 8)) + list(range(-ev, 0, 8)) + list(range(-2*ev, -80, 8))
for index in range(0, len(ages)):
# Comptes I1 à I10 en ligne continue...
if index < len(ages) / 3:
sum_zero_rel_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), ax=ax)
elif index >= (len(ages) / 3) and (index < (len(ages) / 3) * 2):
sum_zero_rel_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[6, 2], ax=ax)
else:
sum_zero_rel_accounts_in_time_160.plot(kind='line', x='Année', y=f'I%d' % (index + 1), dashes=[2, 2], ax=ax)
sum_zero_rel_accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne', style='--', color='black', ax=ax)
sum_zero_rel_accounts_in_time_160.plot(kind='line', x='Année', y='Moyenne Pleine', style='--', color='green', ax=ax)
plt.legend(loc='upper left')
plt.show()

Idem pour ce référentiel. Lorsque les générations se renouvellent de telle manière que N est stable, alors la moyenne est stable.
(e) Etablir les variations relatives long terme des prix d’une valeur quelconque¶
Moyenne des prix en € du m² à Paris (appartements T1 à T4)¶
# Chargement fichier prix immobilier Paris en Euros
estate = pd.read_csv("immobilier_prix_1991-2019.csv", usecols=[1,12], parse_dates=['Année'])
# Moyenne des prix par année
estate_mean = estate.groupby(['Année']).mean()
# Affiche tableur
#display(estate_mean)
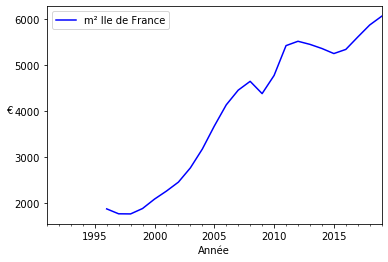
Graphique immobilier en ۦ
# Courbes sur le même graphique
ax = plt.gca()
estate_mean.plot(kind='line', y='IledeFrance', label='m² Ile de France', color='blue', ax=ax)
ax.set_ylabel('€',rotation=0)
plt.show()
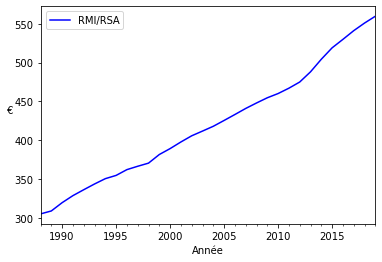
RMI/RSA en ۦ
# Chargement fichier RMI/RSA en Euros
rmi_rsa = pd.read_csv("RMI_RSA_euros_1988-2019.csv", parse_dates=['Année'])
# Moyenne par année
rmi_rsa_mean = rmi_rsa.groupby(['Année']).mean()
# Affiche tableur
#display(rmi_rsa_mean)
Graphique RMI/RSA en ۦ
# Courbes sur le même graphique
ax = plt.gca()
rmi_rsa_mean.plot(kind='line', y='RMI/RSA', color='blue', ax=ax)
ax.set_ylabel('€',rotation=0)
plt.show()
Tableur prix de l’immobilier en RMI/RSA¶
# Capture colonne RMI/RSA en €
rmi_rsa_mean_series = rmi_rsa_mean['RMI/RSA']
# Nouveau tableur
estate_by_rsa = estate_mean.copy()
# Diviser le prix immo par le RSA
estate_by_rsa['IledeFrance'] = estate_by_rsa['IledeFrance'].div(rmi_rsa_mean_series).astype('float64')
Graphique prix de l’immobilier en RMI/RSA¶
# Courbes sur le même graphique
ax = plt.gca()
estate_by_rsa.plot(kind='line', y='IledeFrance', label='m² Ile de France / RSA', color='blue', ax=ax)
ax.set_ylabel('m² Ile de France / RSA', rotation=0, labelpad=60)
plt.show()
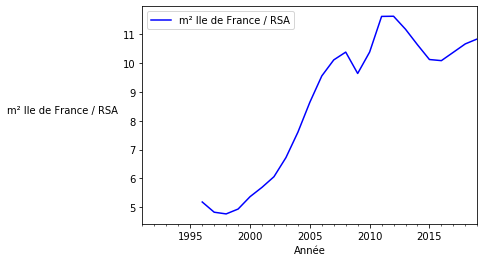
La courbe de la valeur de l’immobilier en RSA ressemble fortement à celle mesurée en €. C’est une très mauvaise nouvelle pour les bénéficiaires du RSA, car cela signifie que le RSA ne tient pas compte de l’inflation des prix de l’immobilier dans sa réévaluation annuelle.
Autrement dit, les bénéficiaires du RSA doivent compter sur d’autres sources de revenus pour se loger…
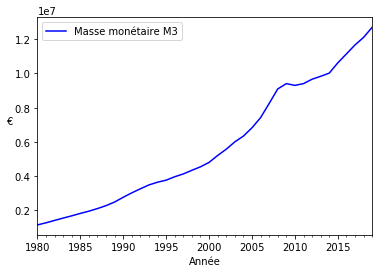
Tableur masse monétaire M3 en €¶
# Chargement fichier masse monétaire M3 en €
monetary_mass = pd.read_csv("masse_monétaire_m3_1980-2019.csv", usecols=[12,13], parse_dates=['TIME_PERIOD'])
# Moyenne par année
monetary_mass_mean = monetary_mass.groupby(monetary_mass['TIME_PERIOD'].dt.to_period("Y")).mean()
# Convertir l'index de PeriodIndex à DatetimeIndex
monetary_mass_mean.index = monetary_mass_mean.index.astype('datetime64[Y]')
# Affiche tableur
#display(monetary_mass_mean)
Graphique masse monétaire M3¶
# Courbes sur le même graphique
ax = plt.gca()
monetary_mass_mean.plot(kind='line', y='OBS_VALUE', label='Masse monétaire M3', color='blue', ax=ax)
ax.set_ylabel('€', rotation=0)
ax.set_xlabel('Année')
plt.show()
Tableur prix de l’immobilier proportionnellement à 10% de la masse monétaire M3¶
# capture colonne masse monétaire en €
monetary_mass_mean_series = monetary_mass_mean['OBS_VALUE'][11:]
# 10% des valeurs
monetary_mass_mean_series_10_percent = monetary_mass_mean_series.mul(0.1).astype('float64')
# Nouveau tableur
estate_by_monetary_mass = estate_mean.copy()
# Prix immobilier / 10% M3 * 100
estate_by_monetary_mass['IledeFrance'] = estate_by_monetary_mass['IledeFrance'].div(monetary_mass_mean_series_10_percent).astype('float64')
# Affiche tableur
#display(estate_by_monetary_mass)
Graphique prix de l’immobilier proportionnellement à 10% de la masse monétaire M3¶
# Courbes sur le même graphique
ax = plt.gca()
estate_by_monetary_mass.plot(kind='line', y='IledeFrance', label='m² Ile de France / 10% M3', color='blue', ax=ax)
ax.set_ylabel('m² Ile de France / 10% M3', rotation=0, labelpad=80)
ax.set_xlabel('Année')
plt.show()
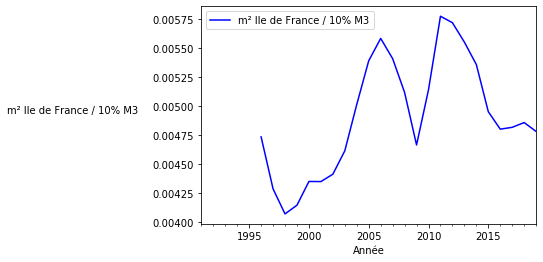
Mesuré en pourcentage de la masse monétaire M3, l’immobilier est très instable, son prix chute fortement après la crise de 2008, et malgré une rebond record en 2013, est en baisse depuis lors.
On constate ici que le prix de l’immobilier entre 2013 et 2019 est en hausse en € et en baisse en proportion de la masse monétaire M3. Cela signifie que changer d’unité de mesure c’est changer de référentiel et que toute affirmation telle “c’est en hausse” ou “c’est en baisse” ne veut rien dire si on ne précise pas dans quel référentiel…
Tableur cours de l’or en €¶
# Chargement fichier cours de l'or en $
gold_once_dollar = pd.read_csv("AUX-USD-2592000-20150729210958.csv", usecols=[0,7], parse_dates=['Date'])
# Chargement fichier cours du dollar en €
dollar_euro = pd.read_csv("eurofxref-hist.csv", usecols=[0,1], parse_dates=['Date'])
# Moyenne par année
gold_once_dollar_mean = gold_once_dollar.groupby(gold_once_dollar['Date'].dt.to_period("Y")).mean()
dollar_euro_mean = dollar_euro.groupby(dollar_euro['Date'].dt.to_period("Y")).mean()
# Ajoute colonne prix de l'or en euros
gold_once_dollar_euro_mean = gold_once_dollar_mean
gold_once_dollar_euro_mean['Euros'] = gold_once_dollar_mean['Close (troy oz)'].mul(dollar_euro_mean['USD'])
# Convertir l'index de PeriodIndex à DatetimeIndex
gold_once_dollar_euro_mean.index = gold_once_dollar_euro_mean.index.astype('datetime64[Y]')
# Affiche tableur
#display(gold_once_dollar_euro_mean)
Graphique cours de l’or en €¶
# Courbes sur le même graphique
ax = plt.gca()
gold_once_dollar_euro_mean.plot(kind='line', y='Euros', label='Once d\'or', color='blue', ax=ax)
ax.set_ylabel('€', rotation=0)
ax.set_xlabel('Année')
plt.show()
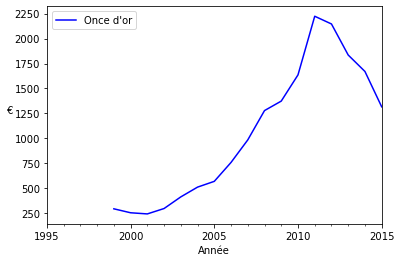
Pour mesurer une valeur A (m² de l’immobilier) dans une unité B (once d’or), il me faut un référentiel commun C. Puisque nous disposons du prix de l’immobilier (valeur A) en € (valeur C), pour pouvoir le mesurer en onces d’or (valeur B), il me faut la valeur B mesurée par C. Au départ, nous n’avons que la valeur B (once d’or) mesuré en dollars (valeur D). Il me faut la mesure de D (dollar) transposée dans le référentiel C (€). Il me faut donc le cours du dollar (valeur D) en € (valeur C).
Nous calculons donc d’abord le prix de l’once d’or en € (valeur B mesurée en C), avant de pouvoir calculer le prix de l’immobilier en once d’or (valeur A mesurée en B).
Tableur prix de l’immobilier en once d’or¶
# Capture colonne once d'or en € de 1991 à 2015
gold_once_dollar_euro_mean_series = gold_once_dollar_euro_mean['Euros'][4:]
# Nouveau tableur
estate_by_gold_ounce = estate_mean.copy()
# Prix immobilier / once d'or
estate_by_gold_ounce['IledeFrance'] = estate_by_gold_ounce['IledeFrance'].div(gold_once_dollar_euro_mean_series).astype('float64')
# Affiche tableur
#display(estate_by_gold_ounce)
Graphique prix de l’immobilier en once d’or¶
# Courbes sur le même graphique
ax = plt.gca()
estate_by_gold_ounce.plot(kind='line', y='IledeFrance', label='m² Ile de France / Once d\'or', color='blue', ax=ax)
ax.set_ylabel('m² Ile de France / Once d\'or', rotation=0, labelpad=80)
ax.set_xlabel('Année')
plt.show()
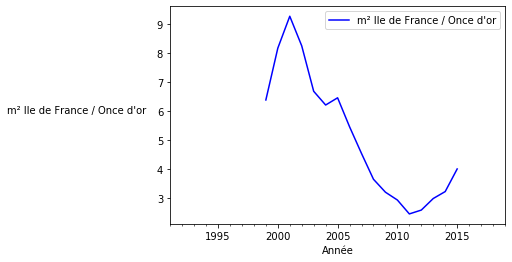
Le prix de l’immobilier en once d’or voit une baisse vertigineuse de sa valeur entre 2001 et 2011. C’est le contraire de sa valeur en € qui est en hausse sur la même période.
Ainsi, peut-on encore affirmer un point de vue unique, absolu sur la hausse ou la baisse de l’immobilier ?
Les changements de référentiel révèlent la nature relative de toutes mesures. Et la “valeur des choses” n’y échappe pas. Estimer la valeur de quelque chose c’est exprimer une mesure dans une unité précise étalonnée par rapport à un référentiel précis. Ainsi avant toute affirmation péremptoire du type “l’immobilier est en hausse”, il convient de toujours préciser dans quelle unité de mesure, selon quel référentiel.
Conclusion¶
Ce module nous a permis de découvrir :
La symétrie spatiale de la monnaie libre.
La symétrie temporelle de la monnaie libre.
Les effets des échanges en monnaie libre.
Le comportement différent de la monnaie selon le référentiel choisi.
Le comportement toujours identique du système, pour un même référentiel, sur plusieurs générations.
La relativité des valeurs, et le besoin d’un référentiel pour toute mesure.
Vincent Texier, Licence CC-BY-SA
4.0
Réalisé avec JupyterLab 
